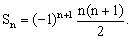高中数学:数列求和的方法
2018-12-24 17:35:09 浏览:1564
一、倒序相加法
此法来源于等差数列求和公式的推导方法。
例1、已知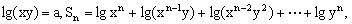 求
求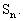
解: 。①
。①
把等式①的右边顺序倒过来写,即①可以写成以下式子:
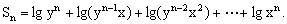 ②
②
把①②两式相加得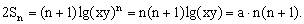
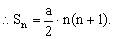
二、错位相消法
此法来源于等比数列求和公式的推导方法。
例2、求数列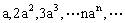 的前n项和。
的前n项和。
解:设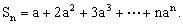
当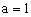 时,
时,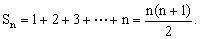
当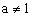 时,
时,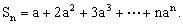 ①
①
①式两边同时乘以公比a,得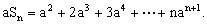 ②
②
①②两式相减得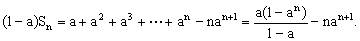
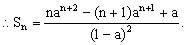
三、拆项分组法
把一个数列分拆成若干个简单数列(等差数列、等比数列),然后利用相应公式进行分别求和。
例3、求数列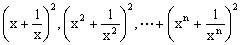 的前n项和。
的前n项和。
解:设数列的前n项和为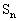 ,则
,则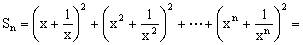
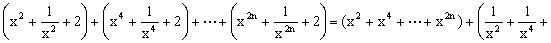
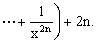
当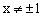 时,
时,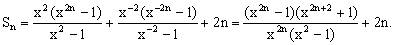
当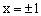 时,
时,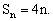
小贴士:在运用等比数列的前n项和公式时,应对q=1与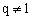 的情况进行讨论。
的情况进行讨论。
四、裂项相消法
用裂项相消法求和,需要掌握一些常见的裂项技巧。如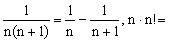
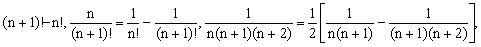

例4、求数列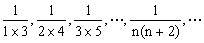 的前n项和。
的前n项和。
解:

五、奇偶数讨论法
如果一个数列为正负交错型数列,那么从奇数项和偶数项分别总结出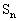 与n的关系进行求解。
与n的关系进行求解。
例5、已知数列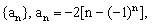 求该数列的前n项和
求该数列的前n项和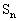 。
。
解: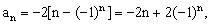 对n分奇数、偶数讨论求和。
对n分奇数、偶数讨论求和。
①当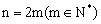 时,
时,
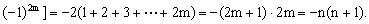
②当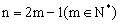 时,
时,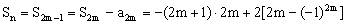
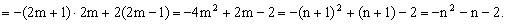

六、通项公式法
利用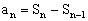 ,问题便转化成了求数列
,问题便转化成了求数列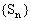 的通项问题。
的通项问题。
例6、已知数列 求该数列的前n项和
求该数列的前n项和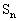 。
。
解: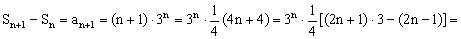
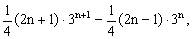 即
即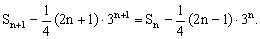
∴数列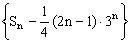 是一个常数列,首项为
是一个常数列,首项为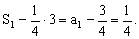

七、综合法
尽量把给定数列转化为等差或等比数列来处理。
例7、已知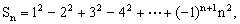 求
求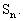
分析:注意观察到: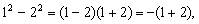
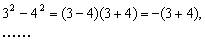
其他可依次类推。关键是注意讨论最后的n是奇数还是偶数。
解:①当n为奇数时,由以上的分析可知:

②当n为偶数时,可知:
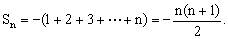
由①②可得