长沙克立兹外国语学校小编整理了高中数学立体几何学习常用公式及结论！ 大家有需求的可以收藏哦！

一、线线平行的判断：

① 如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线和交线平行。

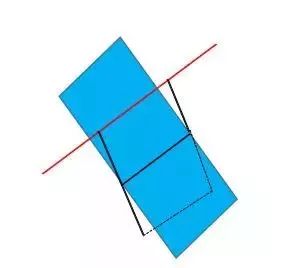
直线和交线平行图

② 如果两个平行平面同时和第三个平面相交，那么它们的交线平行。

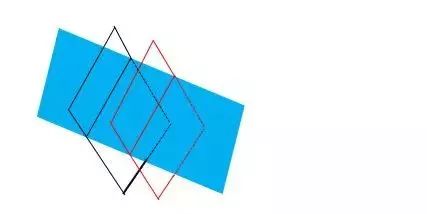
交线平行图

③ 垂直于同一平面的两条直线平行。

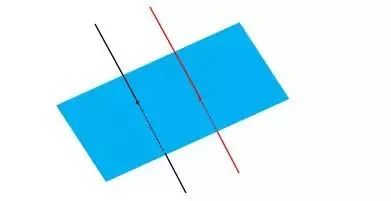
直线平行图

二、 线线垂直的判断：

① 在平面内的一条直线，如果和这个平面的一条斜线的射影垂直，那么它也和这条斜线垂直。

② 在平面内的一条直线，如果和这个平面的一条斜线垂直，那么它和这条斜线的射影垂直。

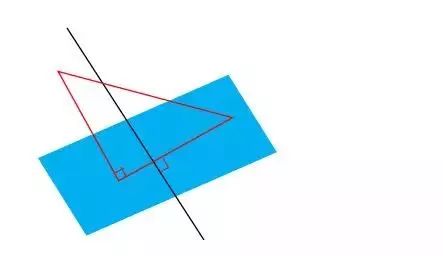
线线垂直图

③ 若一直线垂直于一平面，这条直线垂直于平面内所有直线。

补充：一条直线和两条平行直线中的一条垂直，也必垂直平行线中的另一条。

三、 空间角的求法：（所有角的问题最后都要转化为解三角形的问题，尤其是直角三角形）

① 异面直线所成的角：

通过直线的平移，把异面直线所成的角转化为平面内相交直线所成的角。

异面直线所成角的范围：0° < α ≤ 90°；

注意：

若异面直线中一条直线是三角形的一边，则平移时可找三角形的中位线。有的还可以通过补形，

如：将三棱柱补成四棱柱；将正方体再加上三个同样的正方体，补成一个底面是正方形的长方体。

② 线面所成的角：

斜线与平面所成的角：斜线与它在平面内的射影所成的角。

范围0° < α < 90°

③ 二面角：

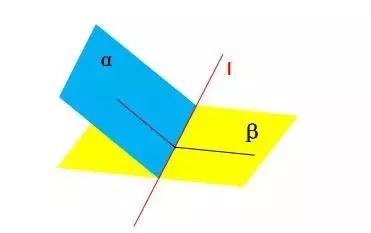
二面角图

关键是找出二面角的平面角。

方法有：①定义法；②三垂线定理法；③垂面法；

定义法：

以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线所成的角叫做二面角的平面角。

还可以用射影法：

cosθ = S'/S ；其中 θ 为二面角 α - l - β 的大小 。

S 为 α 内的一个封闭几何图形的面积；S' 为 α 内的一个封闭几何图形在 β 内射影图形的面积 。

四、 线面平行的判断：

① 如果平面外的一条直线和平面内的一条直线平行，那么这条直线和这个平面平行。

② 两个平面平行，其中一个平面内的直线必平行于另一个平面。

五、 面面平行的判断：

① 一个平面内的两条相交直线分别平行于另一个平面内两相交直线，这两个平面平行。

② 垂直于同一条直线的两个平面平行。

六、 线面垂直的判断：

① 如果一直线和平面内的两相交直线垂直，这条直线就垂直于这个平面。

② 如果两条平行线中的一条垂直于一个平面，那么另一条也垂直于这个平面。

③ 一直线垂直于两个平行平面中的一个平面，它也垂直于另一个平面。

④ 如果两个平面垂直，那么在—个平面内垂直于交线的直线必垂直于另—个平面。

七、 面面垂直的判断：

一个平面经过另一个平面的垂线，这两个平面互相垂直。

八、夹角公式：

空间直角坐标系

夹角公式图

线线夹角公式图

线面夹角公式图

面面夹角公式图

九、 求点到面的距离的方法：

① 直接法：直接确定点到平面的垂线段长（垂线段一般在二面角所在的平面上）；

② 转移法：转化为另一点到该平面的距离（利用线面平行的性质）；

③ 体积法：利用三棱锥体积公式 。

④ 向量法：

向量法中：点到面的距离公式图

十、空间向量的坐标运算

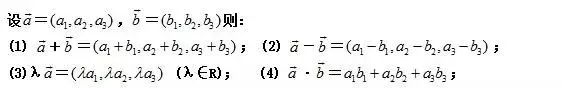
空间向量的坐标运算图

十一、球

① 球的半径是R，则其

球图（1）

② 球的组合体

（1） 球与长方体的组合体：

长方体的外接球的直径是长方体的体对角线长。

（2） 球与正方体的组合体：

正方体的内切球的直径是正方体的棱长；

正方体的棱切球的直径是正方体的面对角线长；

正方体的外接球的直径是正方体的体对角线长。

（3） 球与正四面体的组合体:

棱长为 a 的正四面体的内切球的半径为 (√6 /12) a

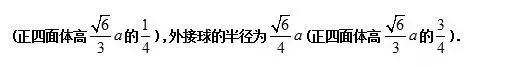
球图（2）

十二、 多面体：

（1）棱柱：两底面互相平行，侧面都是平行四边形，侧棱平行且相等 。

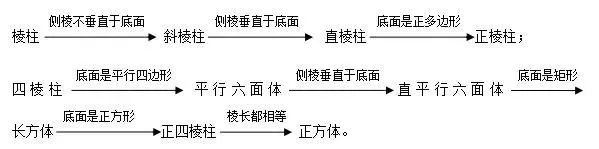
棱柱图

（2）正棱锥：底面是正多边形，侧面是等腰三角形，顶点在底面内的射影是底面中心

性质：

Ⅰ、平行于底面的截面和底面相似；

截面的边长和底面的对应边边长的比等于截得的棱锥的高与原棱锥的高的比；

它们面积的比等于截得的棱锥的高与原棱锥的高的平方比；

截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比；

Ⅱ、各侧面都是全等的等腰三角形；通过四个直角三角形

正棱锥图（1）

实现边，高，斜高间的换算 。

正棱锥图（2）

（3）正四面体：

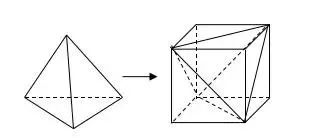
正四面体图（1）

对于棱长为 a 正四面体的问题可将它补成一个边长为 √2/2a 的正方体问题。

对棱间的距离为 √2/2a （正方体的边长）

正四面体的高 √6/3a （= 2/3 × L正方体体对角线）

正四面体的体积为

正四面体图（2）

正四面体的中心到底面与顶点的距离之比为 1 ： 3