实际测量中的有关名称、术语

1测量距离问题的基本类型和解决方案

2测量高度问题的基本类型和解决方案

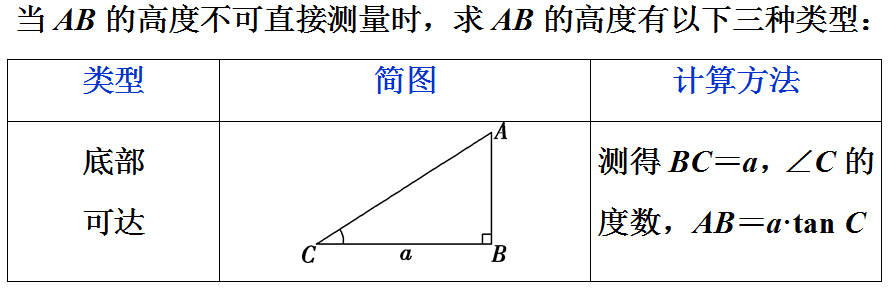
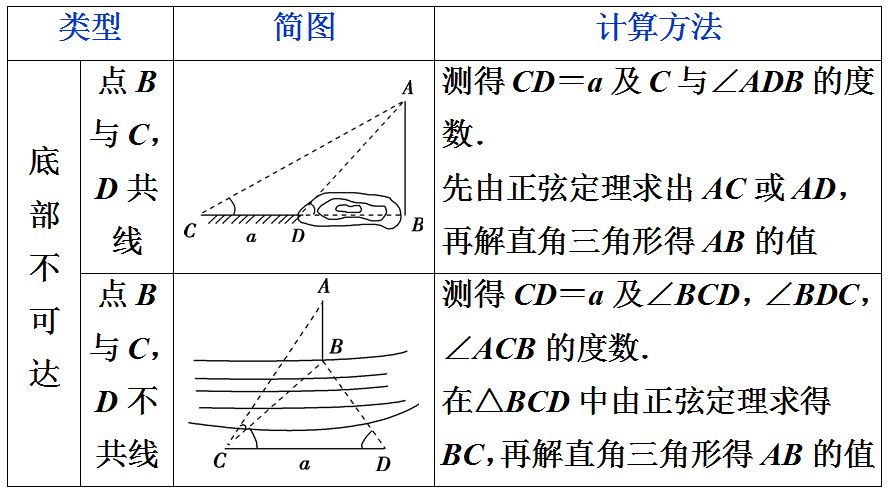
练习题

1.判断正误(正确的打“√”，错误的打“×”)

(1)坡面与水平面所成的二面角称为坡角．()

(2)坡面的水平宽度与坡面的铅直高度之比称为坡度．()

(3)一般来说，在测量过程中基线越长，测量的精确度越低．()

(4)若P在Q的北偏东44°，则Q在P的东偏北44°方向．()

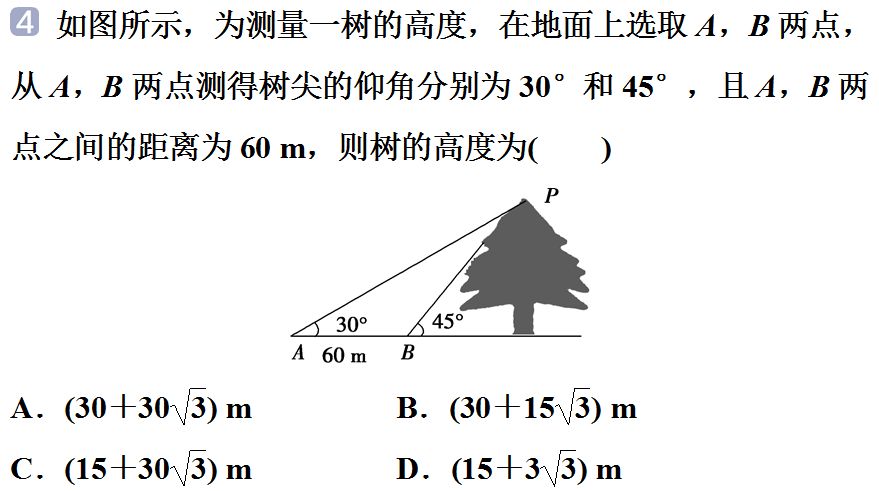
例题一：测量距离问题

测量距离问题的解题思路

测量距离问题一般分为三种类型：①两点间不可达又不可视；②两点间可视但不可达；③两点都不可达．解决此问题的方法是：选择合适的辅助测量点，构造三角形，将问题转化为求某个三角形的边长问题，从而利用正、余弦定理求解．构造数学模型时，尽量把已知元素放在同一个三角形中．

解三角形应用题的一般步骤：

（1）分析：理解题意，分清已知与未知，画出示 意图

（2）建模：根据已知条件与求解目标，把已知量与求解量尽量集中在有关的三角形中，建立一个解三角形的数学模型

（3）求解：利用正弦定理或余弦定理有序地解出三角形，求得数学模型的解

（4）检验：检验上述所求的解是否符合实际意义，从而得出实际问题的解